5+7=-4

Die Integer-Rechenscheibe

Dr. Hermann Puhlmann

Juni 1999

Aufgabenbeschreibung

Natürlich ist 5+7=12, und nicht -4. Nicht einmal auf schlecht programmierten Computern dürfte dieser Fehler auftreten. Dennoch zeigt das Beispiel einen Fehler auf, der in vielen Programmiersprachen vorkommt, wenn auch erst bei größeren Zahlen. So liefert Turbo-Pascal beispielsweise 30000+20000=-15536, und die Haskell-Implementation Hugs rechnet 2000000000+1000000000=-1294967296. Grund dafür sind in jedem Fall Integer-Überläufe, die nicht als Fehler erkannt werden. Ein genaues Verständnis des Phänomens ist aber nur möglich, wenn man um die rechnerinterne Darstellung des Datentyps Integer weiß.

Ziel der hier vorgestellten Integer-Rechenscheibe ist es daher, an einem überschaubaren Beispiel, nämlich 4-Bit Integern, die Darstellung ganzer Zahlen im Rechner zu veranschaulichen. Darüber hinaus soll der Effekt des Integer-Überlaufs ,,begreifbar`` gemacht werden. Dazu können Addition und Subtraktion von Hand an der Scheibe durchgeführt werden.
 

Darstellung ganzer Zahlen im Computer

Zur Darstellung ganzer Zahlen verwenden Programmiersprachen üblicherweise eine feste Anzahl n von Bits. Dabei ist nnormalerweise ein Vielfaches von 8, was der Aufteilung des Computerspeichers in Bytes, d. h. Portionen von je 8 Bits, Rechnung trägt.

Der Übersichtlichkeit halber demonstrieren wir hier die Integer-Darstellung jedoch zunächst mit nur 4 Bits. Damit sind 2⁴=16 verschiedene Werte darstellbar. Untersuchen wir zuerst, welche dezimalen Zahlenwerte hierdurch dargestellt werden.

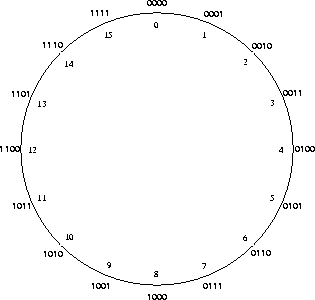
Zunächst kann man die 16 verschiedenen Bitfolgen als Dualzahlen interpretieren. Es ergeben sich dann die korrespondierenden Zahlenwerte von 0 bis 15. Abbildung 1 zeigt die Bitfolgen und diese dezimalen Werte. Die Anordnung im Kreis suggeriert, dass auf die Folge 1111 die Folge 0000 folgt. Dezimal ausgedrückt bedeutet dies, dass auf die Zahl 0 die Zahl 15 folgt. Dies entspricht zwar nicht dem Rechnen mit ganzen Zahlen, es gibt aber genau die Struktur der Restklassen modulo 16 wieder. Dort gilt in der Tat 15+1=0, genauer: 15+1=0 mod 16. Mehr noch: Diese Interpretation der Bitfolgen ist adäquat beim Rechnen mit Integern (wenn keine Fehlermeldung beim Integer-Überlauf erfolgt), und sie erlaubt es auch, die negativen Zahlen zu erfassen.
 

Abbildung 1: Bitfolgen interpretiert als Zahlen von 0 bis 15

Betrachten wir, wieso das Rechnen ohne Überlaufwarnung gerade dem Rechnen modulo 16 entspricht. Als Beispiel addieren wir die Binärdarstellungen von 13 und 5:

1101
+	0101
	10010

Bei der Rechnung tritt ein Übertrag in der führenden Stelle auf. Sind nur 4 Stellen zur Repräsentatin des Ergebnisses vorhanden, und wird dieser Überlauf nicht als Fehler gemeldet, so schneidet der Rechner einfach die führende Stelle des Ergebnisses ab und speichert anstelle der korrekten Bitfolge 10010 die Folge 0010, die den dezimalen Wert 2 hat. Die abgeschnittene Stelle hat den Wert 16, so dass tatsächlich durch das Abschneiden ein Rechnen modulo 16 erreicht wird.

Akzeptiert man einmal, dass nicht mit Z, sondern mit Z₁₆, den ganzen Zahlen modulo 16, gerechnet wird, so ist der Schritt zur Darstellung negativer Zahlen nicht mehr weit. Modulo 16 ist doch die Zahl -1 äquivalent zur 15, genauso -2 äquivalent zur 14 und so weiter. Man kann also vom "oberen Ende" her darstellbare Zahlen wegnehmen und sie in der Interpretation als negative Zahlen "von unten her" dazufügen. Wir teilen die verfügbaren Bitfolgen zwischen negativen und positiven Zahlen auf. So interpretieren wir 1000 als -8 und gehen im Zahlenkreis weiter bis 0111, was die Zahl 7 repräsentiert. 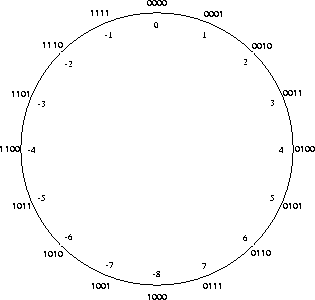Da wir eine Folge (nämlich 0000) zur Darstellung der Zahl 0 brauchen, ist eine völlige Symmetrie zwischen negativen und positiven Zahlen nicht zu erreichen. Abbildung 2 zeigt die neue Zuordnung der Bitfolgen zu Zahlen. Beachten Sie, dass wir hinsichtlich der Restklassen modulo 16 nichts verändert haben. Wir haben lediglich für einige Restklassen andere Repräsentanten gewählt. Damit ist auch klar, dass die Addition genauso durchgeführt wird, wie wir dies oben für das Beispiel 13+5 getan haben. Die Rechnung würde in der neuen Interpretation der Bitfolgen allerdings-3+5 lauten, und plötzlich ist das Ergebnis 2 auch richtig im herkömmlichen Sinne. Tatsächlich mussten wir bei dieser Rechnung den Bereich der Zahlen von -8 bis +7 nicht verlassen, und so stimmt die Rechnung modulo 16 mit der üblichen Rechnung in Z überein.
 

Abbildung 2: Bitfolgen interpretiert als Zahlen von -8 bis 7

Damit sind wir beim letzten Schritt zur Erklärung der Integer-Darstellung. Wir trennen uns nun wieder von der Vorstellung des Restklassenrechnens und behalten lediglich die Zahldarstellung bei. Verlassen wir den Bereich der darstellbaren Zahlen nicht, so können wir korrekt rechnen und müssen nichts über Restklassen wissen. Ein Integer-Überlauf tritt nun aber nicht beim Übergang von 1111 nach 0000 auf, sondern beim Schritt von 0111 nach 1000. Wird hierbei keine Fehlermeldung erzeugt, so ist, wie in der Überschrift, 5+7=-4.

Kommen wir abschließend zurück zur Darstellung ganzer Zahlen mit n anstelle von nur 4 Bit. Die angeführten Überlegungen lassen sich dann direkt übertragen. Es sind dann 2ⁿ Zahlen darstellbar und es wird modulo 2ⁿ gerechnet. Die Bitfolgen werden nicht als die Zahlen von 0 bis 2ⁿ-1 interpretiert, sondern als -2^n-1 bis2^n-1-1. Bei 16 Bit erhält man so die bekannte Spanne von -32768 bis +32767, die dem obigen Beispiel 30000+20000=-15536 für Turbo-Pascal zugrunde liegt. Bleibt man im darstellbaren Bereich, so sind die Rechnungen auch in Z korrekt. Beim Überschreiten der Bereichsgrenzen zeigt sich jedoch, dass streng genommen in Z₂n gerechnet wurde.
 

Aufbau und Funktion der Rechenscheibe

Die Rechenscheibe besteht aus zwei konzentrischen Kreisscheiben aus 0,5mm starker Folie, die in ihrem Mittelpunkt durch eine Niete als Scharnier verbunden sind. Die untere, größere Scheibe hat einen Radius von ca. 8cm und ist farblos, die obere, kleinere Scheibe ist transparent eingefärbt und hat einen Radius von ca. 6cm. Auf die genauen Maße kommt es dabei nicht an, die Scheiben sollten aber gut mit einem Overhead-Projektor projizierbar sein.

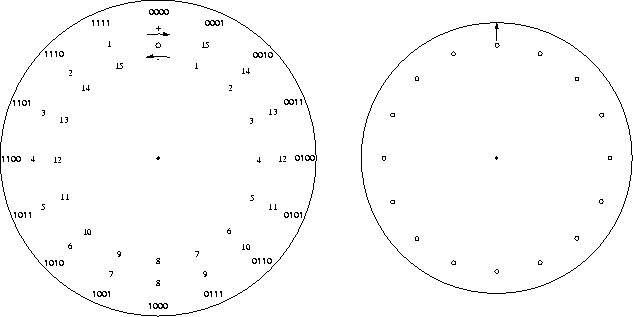
Auf der großen Scheibe sind die Bitfolgen von 0000 bis 1111 im Kreis eingetragen, außerdem die den Bitfolgen (außer der 0000) entsprechenden Zahlen von 1 bis 15 (als Subtraktionsskala) sowie ihre jeweiligen Komplemente zur 16 (als Additionsskala). Die Additions- und die Subtraktionsskala sind durch entsprechende Pfeile gekennzeichnet. Zudem ist bei der Bitfolge 0000 ein kleines Anschlagsloch eingestanzt, dessen Funktion durch das Zusammenspiel mit der kleinen Scheibe erklärt wird.

Am Rand der kleinen Scheibe sind in gleichen Abständen 16 kleine Löcher eingestanzt, die zur Führung des Rechenstifts bei der Addition und der Subtraktion dienen. Ferner ist an einem der Löcher ein Ablesepfeil angebracht. Abbildung 3 zeigt den Aufbau beider Scheiben.

Abbildung 3: Der Aufbau der beiden Teilscheiben der Rechenscheibe

Die Bedienung der Scheibe erfolgt mit einem Zahnstocher als Rechenstift. Als Beispiel sei die Durchführung der Berechnung von 5+7 dargestellt. Hierzu bringt man die Scheibe zunächst in die Ausgangsstellung, in der der Ablesepfeil der kleinen Scheibe auf die 0000 der großen Scheibe zeigt. Nun gibt man die Zahl 5 ein, indem man den Zahnstocher in das Loch neben der 5 der Additionsskala steckt und in Richtung des Additonspfeiles dreht, bis der Zahnstocher im Anschlagsloch der großen Scheibe einrastet. Nun addiert man auf analoge Weise die Zahl 7. Der Ablesepfeil zeigt danach auf die Bitfolge 1100, die als 12 oder -4 interpretiert wird.

Zur Subtraktion verwendet man in analoger Weise die Subtraktionsskala.
 

Unterrichtliche Verwendung der Rechenscheibe

Die Rechenscheibe ist so gestaltet, dass sie gut projiziert werden kann, aber genauso individuell am Arbeitsplatz einzelner Schüler oder Schülergruppen verwendet werden kann. Außerdem ist es leicht, selbst solche Scheiben zu bauen, ggf. auch aus anderen Materialien.

Im Folgenden sollen zwei Varianten der Verwendung der Rechenscheibe dargestellt werden.

Die Rechenscheibe zur Erklärung falscher Integer-Ergebnisse

Einen natürlichen Einstieg zur Behandlung der Zahldarstellung im Computer bieten Computerprogramme (gleich in welcher Sprache), die beim Rechnen mit ,,ganzen Zahlen`` wegen eines nicht erkannten Überlaufs falsche Ergebnisse liefern. Beim Beispiel 30000+20000=-15536 etwa kann man untersuchen, ob der "Abstand" von 30000 zu -15536 gerade 20000 ist, wenn man die Integer-Zahlen an beiden Enden "zusammenklebt", also auf 32767 die Zahl -32768 folgen lässt. Der Erfolg dieser Untersuchung gibt Anlass, die Zahldarstellung genauer zu betrachten.

Um den Datenbereich vollständig überblicken zu können, wird die Reduktion auf 4 Bit vorgenommen. Dann können an der Rechenscheibe auch Rechnungen ausgeführt werden, bei denen ein Überlauf eintritt. Dabei ist es sinnvoll, beide Interpretationen der Bitfolgen (0 bis 15 oder -8 bis 7) zu betrachten, da hierdurch die einende Sichtweise des Rechnens modulo 16 klar wird. Aus diesem Grund sind auf der Rechenscheibe diese Interpretationen nur in der Additions- und Subtraktionsskala versteckt gehalten. Auf der äußeren Skala sind dagegen die Bitfolgen angegeben, die noch beide Deutungen zulassen.

Anregend kann nun die Fragestellung nach anderen Darstellungen der ganzen Zahlen sein. Beispielsweise besteht die Möglichkeit, n-1 von n Bit für die Darstellung des Betrags einer Zahl in der üblichen Binärdarstellung zu verwenden und das n-te Bit als Vorzeichenbit zu verwenden. Dann ist es leichter, zu einer Bitfolge die Dezimaldarstellung zu bestimmen. Dagegen wird es viel schwieriger, Operationen auf dem Datentyp durchzuführen. Die Eleganz der Darstellung durch Repräsentanten modulo 2ⁿ tritt durch die Einfachheit des Addierens und Subtrahierens mit der Scheibe zu Tage.

Ist das Prinzip gut verstanden, so kann der Schritt zurück zu 16- oder 32-Bit Integern gemacht werden, indem die Anordnung der Zahlen in einem Kreis schematisch dargestellt wird. Hier können Addition und Subtraktion nun im Geiste vollzogen werden, da das Bild des Weiterdrehens der im Kreis angedordneten Zahlen noch präsent ist.

Schüler erfinden die Rechenscheibe selbst

Ein anderer Zugang zum Thema Zahldarstellung im Computer besteht darin, die Schüler die Rechenscheibe noch einmal selbst erfinden und bauen zu lassen. Einen Einstieg dazu bietet ein "Rechenschieber" aus zwei Linealen, mit denen Additionen kleiner Zahlen durchgeführt werden können. Die Aufgabe, Winkelsummen zu berechnen oder nur die letzten beiden Stellen des Ergebnisses zu bestimmen, führt automatisch zu einer kreisförmigen Skalenanordnung. Der Schritt zu 16 durch 4 Bit darstellbare Zahlen und ihrer kreisförmigen Anordnung ist nun nicht mehr weit. Hier werden die Schüler verschiedene Bauformen der Rechenscheibe erfinden. So ist eine statische Bauform denkbar, in der zwei gleiche Skalen gegeneinander verdreht werden. Es wird dort in der Weise gerechnet, die vom Multiplizieren mit dem logarithmischen Rechenschieber her bekannt ist. Die Anregung, Additionen mit mehr als zwei Summanden durchführen zu wollen, führt dann aber auch leicht auf die von mir entworfene dynamische Variante, in der jede Rechnung mit einer Bewegung verbunden ist, an deren Ende ein Pfeil das Ergebnis anzeigt.

Mit einer solchen selbstgebauten Rechenscheibe lassen sich auch Subtraktionen durchführen, die ein negatives Ergebnis haben (auch wenn dies ursprünglich nicht als Anforderung benannt war). Lenkt man die Aufmerksamkeit noch darauf, dass sich in üblichen Programmiersprachen der Datentyp Integer nicht von 0 bis 65536, sondern von -32768 bis 32767 erstreckt, so können Schüler die Zahldarstellung im Computer selbst entdecken: Zuerst für die Zahlen von -8 bis 7 bei einer 4-Bit Darstellung, dann aber auch für den Datentyp Integer in realen Programmiersprachen.
 

Beschreibung der beigelegten Fotos

Die beigelegten Fotos (auf der Rückseite mit "Bild 1" bis "Bild 4" gekennzeichnet) zeigen die Rechenscheibe. Dabei zeigen die ersten drei Bilder die Aufsicht auf die Scheibe mit den drei Einstellungen, die beim Durchführen der Rechnung 5+7=+4 auftreten. Bild 4 zeigt die Projektion der Scheibe mit einem Overhead-Projektor.

Benutzer: gast • Besitzer: schwill • Zuletzt geändert am: